|
| Feeling....Angry? |
Angry Birds: Owned...... with math????
“Awww
maaaan. I still can’t beat this stupid level!! Forget it I give up. Those
stupid pigs can have the stupid eggs I would have eaten them too.” Sound
familiar? If not think about all the frustration angry birds has given you,
every level that seemed just impossible to beat or to get that third golden
star……done? Well guess what, I have a solution that will get you perfect scores
on every single level of angry birds you will ever play. But you’re going to
have to put in a little effort…and a little math.
Now
wait just one second before you go clicking that back button. That’s right
Ernie, get your hand off the mouse and listen for a moment.
Think about it. How do you think you may have won levels in the past? You’re probably thinking, “Um, by shooting the bird?” Well, duh. The point is that you had to angle the bird a certain way in order to hit your target. “Are you serious? Anyone can figure that out.” Well then Einstein, did you ever notice the little trail your birds left after missing the target (again…..)? You can use this to your advantage and will never have to lose another thing ever again (in angry birds of course. Sadly this doesn’t fix relationships. I mean, isn't is your fault that you spent your life on this game rather than paying attention to the love of your life? Yeah, smooth move pulling this game out on your honeymoon. >_>)
Anyways, this game can be solved with a special section of Algebra called: Quadratics. Don’t worry I won’t bore you with long college lectures on how to do this. Actually, after learning a few basic things, you will completely own this game. (Does not apply to Angry Birds Space). So whether you are old or young, I will teach how to beat Angry Birds with a method developed by high school ki...I mean developed by experts. So be prepared to start of the road to victory, and finally getting those eggs. (And finally being able to move on with your life.) Still here? Good, let's dive into it.
Take it a step at a time
Introduction
Many of our readers have played the immensely popular Angry
Birds game at some point in the past year. We're here to show you how you, yes,
you, can beat the game every single time.
First off, you need to know the basic shape of the flight path
of the birds. Can you guess? If you guessed the parabola, then you're right!
The game is laid out like a coordinate grid, and the parabola is situated on
that grid. So, hypothetically, if we were to create an equation on that grid to
calculate the bird's flight path, then we, in theory, should be able to
flawlessly beat the game.
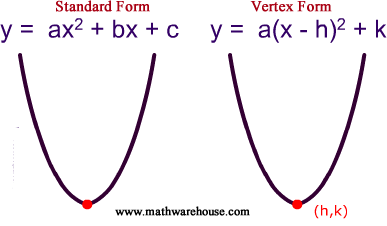
How do we use the parabola, you ask? Well, first off, you
need to know that the equation for the parabola is y = ax2 + bx+ c. This form
is called the Standard Form.
Rules of the Standard Form:
The role of 'a'
if a> 0, the parabola opens
upwards
With this screenshot, you should be able to
locate a plot of imaginary axes. Once this is located, you can easily determine
your "a" variable, as it is the variable that you can control; the
more tilted the bird's angle is, the higher the "a" variable. There
is also another variable that you can control. The "k" variable
varies with how long you have you have your bird pulled back, and at what angle
you have the flight set to. The steeper and longer it is, the more your
"k" variable becomes. This increases your vertical shift, or,
decreases it. With this knowledge, you
can, in your head, determine the overall flight path of the bird, and actually
be able to hit your target.
if a< 0, it opens downward
The axis of symmetry The axis of symmetry is the line x = -b/2a (Click the link for a more detailed explanation)
The role of "c"
The axis of symmetry The axis of symmetry is the line x = -b/2a (Click the link for a more detailed explanation)
The role of "c"
"c" determines the vertical shift
of the graph, or how high or low the graph is compared to the origin.
Another way you might
see this equation written is as y = a(x-h)2+k. This is called the
Vertex Form.
Rules of the Vertex Form:
(h,k) is the vertex
If a is
positive then the parabola opens upwards like a regular "U".
If a is
negative, then the graph opens downwards like an upside
down "U".
If |a|
< 1, the graph of the parabola widens. This just means that the
"U" shape of parabola stretches out sideways.
If |a|
> 1, the graph of the graph becomes narrower(The effect is the opposite of
|a| < 1).
So, how does all of this math help you win? It's rather
simple really; you just have to be able to formulate a quadratic equation that
allows for the bird's fight path to accurately hit the pigs. We'll show you
how.
Graphs/Equations/Methods
Before you start working out the problem, you must first
have your x and y axes labeled and properly scaled. For ease, your x-axis
should be situated where your bird starts. Once this is done, you should create
gridlines for graphing. Next, look and see where your bird is situated based on
your graph. Then, look and see where the pig is situated on your graph. You
have to know these points. These points, if they are situated on your x-axis,
are your roots, and with them, you can calculate the vertex form of the
quadratic function. How do you do this? Simple. Your roots, the x-values of the
x-intercept, are, in actuality, opposites of the factors of your equation. Your
factors are written as (x-h)(x-h). Look familiar? That's because that this is
seen in the vertex form as (x-h)2. Once you have you vertex form,
you can get your standard form quite easily. Simply factor your factors, and
then combine like-terms.